자발적 대칭성 깨짐(Spontaneous Symmetry Breaking, SSB)이란 계의 전체적 대칭성은 깨지지 않았음에도 불구하고 섭동 이론의 관점에서 대칭성이 깨진 것처럼 보이는 것을 가리킨다. SSB를 설명하는 가장 쉬운 방법은 고전역학을 이용하는 것이다.
예를 들어 다음과 같은 퍼텐셜을 생각해보자. (이런 모양의 언덕이 있다고 생각해도 좋다.)
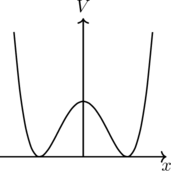
한눈에 보기에도 이 퍼텐셜은 
을 중심으로 좌우 대칭, 즉 
에 대해 불변이다. 그러나 이 퍼텐셜의 특별한 점은 대칭의 중심인 이 불안정하다는 것이다. 만약 중간에 공을 놓는다면, 아주 약간의 흔들림만으로도 공은 좌우 어딘가로 (minimum) 굴러떨어질 것이다. 공이 굴러떨어지고 나면 공에 약간의 흔들림이 있더라도 (섭동) 공이 반대쪽으로 넘어갈 수는 없다.
이제 같은 상황을 섭동적 양자장론의 관점에서 바라보자. 계속 섭동이라는 말을 쓰고 있는데, 그 말의 의미가 무엇인지도 함께 알게 될 것이다. 양자장론에서 진공(vacuum)은 에너지가 가장 낮은 상태를 의미한다. 양자역학에서 말하는 바닥상태와 같은 뜻이라고 보면 된다. 입자(particle)는 양자장이 특정 방법으로 들뜬 상태를 의미하는데, 여기서 ‘특정 방법’이란 간단히 말해 시스템 전체에 큰 영향을 줄 수 없을 정도로 작은 에너지를 가진다는 의미로 받아들이면 편하다. 여기서 섭동이라는 키워드가 중요해지는데, 우리는 양자장론으로 물리 현상을 설명할 때 진공 상태에서 입자들 몇 개가 돌아다니는 상황을 생각한다. ‘입자’는 낮은 에너지를 가지기 때문에 결국 계는 진공 상태에서 그다지 크게 변하지 않는다. 이렇듯 기준이 되는 상태(진공)에서 약간의 변화를 가해 어떤 현상이 일어나는지 알아보는 것을 섭동 이론이라고 한다.
위 설명에서 중요한 부분만 정리해보자.
- 에너지가 가장 낮은 바닥상태를 진공이라고 부른다.
- 입자는 양자장이 작은 에너지로 들뜬 상태를 말한다.
- 우리는 진공에서 크게 벗어나지 않는 상태를 주로 생각한다.
위에 그려진 퍼텐셜에서 바닥상태는 어디일까? 여기서 고전역학과 양자역학의 차이를 볼 수 있다. 간단히 입자가 왼쪽으로 굴러떨어진 상태를 
, 오른쪽으로 굴러떨어진 상태를 
이라 하자. 직관적으로 고전역학이라면 과 은 둘 다 에너지가 가장 낮은 바닥상태이다. 즉, 아래 그림과 같은 상황이다.
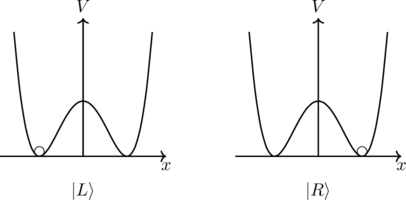
반면 양자역학에서는 양자터널링과 중첩으로 인해 전혀 다른 상황이 된다. 일반적으로 바닥상태의 파동함수는 마디(파동함수의 크기가 0인 지점)이 없으며, 마디 개수가 늘어날수록 에너지가 커진다.
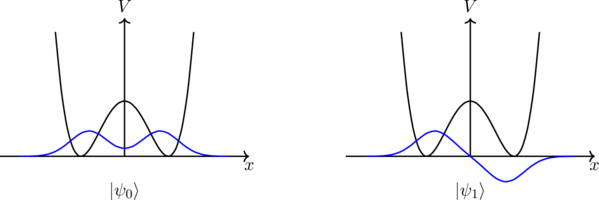
상태 과 은 에너지 고유상태들의 선형 결합으로 나타낼 수 있다. 예를 들어, 위에 나타낸 파동함수를 기준으로
![\[\ket{L}=\frac{1}{\sqrt{2}}(\ket{\psi_{0}}+\ket{\psi_{1}}),\quad\ket{R}=\frac{1}{\sqrt{2}}(\ket{\psi_{0}}-\ket{\psi_{1}})\]](https://research.ssongblog.com/wp-content/ql-cache/quicklatex.com-3f98746695c0ad298739abc645b185ec_l3.png "Rendered by QuickLaTeX.com")
라 써볼 수 있다. 그러면 아래와 같은 상태들이 만들어진다.
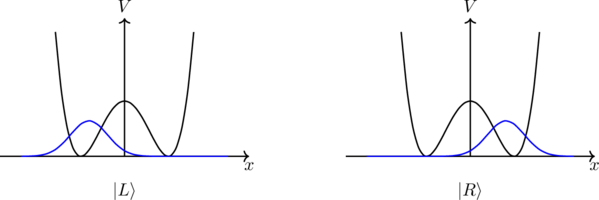
비록 우리가 대칭성이 깨진 상태 과 을 구현해낼 수 있다고 하더라도, 바닥상태인 
에서는 대칭성이 깨지지 않았다. (사실 모든 에너지 고유상태가 그렇다.) 지금까지의 결과를 놓고 볼 때, 양자역학에서는 자발적 대칭성 깨짐이 일어날 수 없는 것으로 보인다. 그렇다면 왜 양자장론에서는 자발적 대칭성 깨짐이 가능한 것일까?
이 질문은 내가 SSB에 대해 처음 배울 때부터 가지고 있었던 질문이었는데, 최근에서야 어느 정도 답을 알게 되었다. (2편으로…)